处理缺失值之多重插补(Multiple Imputation)
带有缺失值的数据在现实中很常见,一般的统计软件只会进行如行删除法(listwise)或叫个案删除(case-wise)来处理缺失值,如果数据集中出现了很多缺失值,很大一部分信息都得删除,那么剩余的样本是否还能反映真实的情况呢?
本文就向大家介绍一种可以利用整个数据集的方法——多重插补。
多重插补(Multiple Imputation)是一种基于重复模拟的处理缺失值的方法。它从一个包含缺失值的数据集中生成一组完整的数据集。每个数据集中的缺失数据用蒙特卡洛方法来填补。
本文使用R语言中的mice包来执行这些操作,首先我们来看mice包的操作思路:
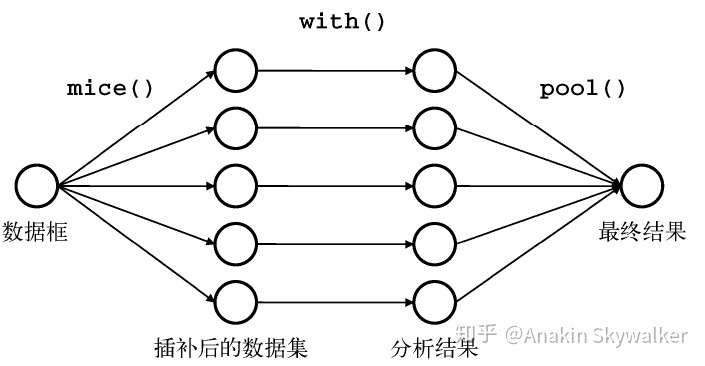
- mice()首先从一个包含缺失数据的数据库开始,返回一个包含多个(默认为5个)完整数据集的对象。每个完整数据集都是通过对原始数据框中的缺失数据进行插补而生成的。由于插补有随机的成分,因此每个完整数据集都略有不同。
- with()函数可依次对每个完整数据集应用统计模型(如线性模型或广义线性模型)。
- pool()函数将这些单独的分析结果整合为一组结果。最终模型的标准误和p值都将准确地反映出由于缺失值和多重插补而产生的不确定性。
基于mice包的分析过程:
library(mice)
imp <- mice(data, m)
fit <- with(imp, analysis)
pooled <- pool(fit)
summary(pooled)data:包含缺失值的矩阵或数据框;
imp:一个包含m个插补数据集的列表对象,同时还含有完成插补过程的信息。默认为5;
analysis:用来设定应用于m个插补数据集的统计分析方法。比如线性回归模型的lm()函数,举个例子lm(Dream ~ Span + Gest),表达式在函数的括号中,~左边是因变量,右边是自变量,用+符号分隔开。这个例子中Dream是因变量,Span和Gest是自变量;
fit:一个包含m个单独统计分析结果的列表对象;
pooled:一个包含m个统计分析平均结果的列表对象。
现将多重插补法运用到sleep数据集上,sleep数据集中包含62种哺乳动物的睡眠、生态学变量和体质变量间的关系。
library(mice) # 载入mice包
data(sleep,package = "VIM") # 载入VIM包中的sleep数据集
imp <- mice(sleep, seed = 1234) # 创建包含默认5个插补数据集的列表
iter imp variable
1 1 NonD Dream Sleep Span Gest
1 2 NonD Dream Sleep Span Gest
1 3 NonD Dream Sleep Span Gest
1 4 NonD Dream Sleep Span Gest
1 5 NonD Dream Sleep Span Gest
2 1 NonD Dream Sleep Span Gest
2 2 NonD Dream Sleep Span Gest
2 3 NonD Dream Sleep Span Gest
2 4 NonD Dream Sleep Span Gest
2 5 NonD Dream Sleep Span Gest
3 1 NonD Dream Sleep Span Gest
3 2 NonD Dream Sleep Span Gest
3 3 NonD Dream Sleep Span Gest
3 4 NonD Dream Sleep Span Gest
3 5 NonD Dream Sleep Span Gest
4 1 NonD Dream Sleep Span Gest
4 2 NonD Dream Sleep Span Gest
4 3 NonD Dream Sleep Span Gest
4 4 NonD Dream Sleep Span Gest
4 5 NonD Dream Sleep Span Gest
5 1 NonD Dream Sleep Span Gest
5 2 NonD Dream Sleep Span Gest
5 3 NonD Dream Sleep Span Gest
5 4 NonD Dream Sleep Span Gest
5 5 NonD Dream Sleep Span Gest我们看看imp的汇总信息
summary(imp)
Multiply imputed data set
Call:
mice(data = sleep, seed = 1234)
Number of multiple imputations: 5
Missing cells per column:
BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
0 0 14 12 4 4 4 0 0 0
Imputation methods:
BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
"" "" "pmm" "pmm" "pmm" "pmm" "pmm" "" "" ""
VisitSequence:
NonD Dream Sleep Span Gest
3 4 5 6 7
PredictorMatrix:
BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
BodyWgt 0 0 0 0 0 0 0 0 0 0
BrainWgt 0 0 0 0 0 0 0 0 0 0
NonD 1 1 0 1 1 1 1 1 1 1
Dream 1 1 1 0 1 1 1 1 1 1
Sleep 1 1 1 1 0 1 1 1 1 1
Span 1 1 1 1 1 0 1 1 1 1
Gest 1 1 1 1 1 1 0 1 1 1
Pred 0 0 0 0 0 0 0 0 0 0
Exp 0 0 0 0 0 0 0 0 0 0
Danger 0 0 0 0 0 0 0 0 0 0
Random generator seed value: 1234 Number of multiple imputations: 5 表示多重插补的数量,5次;
Missing cells per column表示每列变量缺失值包含的数量,如NonD包含14个缺失值;
Imputation methods可以看出对于有缺失值的变量采用了pmm(预测均值)的方法来插补。BodyWgt、BrainWgt、Pred、Exp、Danger没有进行插补,因为这些变量没有缺失数据;
VisitSequence从左至右展示了插补的变量,这里进行插补的分别是sleep数据集中的第3到7列变量;
PredictorMatrix是预测变量矩阵,行代表插补变量,列代表为插补提供信息的变量,1和0表示使用和未使用。NonD到Gest这5行有缺失值,所以只有这5行进行了插补,每个含有缺失值的变量都利用了其他变量提供的信息来进行插补;
Random generator seed value: 1234 是设定种子数,为了让你的结果和我分析的结果一样。
通过提供imp的子成分,可以观测到实际的插补值。
imp$imp$Span
1 2 3 4 5
4 4.7 7.0 2.0 28.0 4.5
13 7.0 13.0 18.0 4.5 13.7
35 14.0 7.0 12.7 13.7 24.0
36 2.6 4.7 4.5 5.0 4.5可以看到Span(寿命)这个变量的5次插补值。检查该矩阵可以帮助你判断插补值是否合理。
利用complete()函数可以观察m个插补数据集中的任意一个。
complete(imp, action = #) # 括号内的#指的是m个完整数据集中哪一个我们可以查看5个完整数据集中的第2个数据集,并将其赋值给dataset2
dataset2 <- complete(imp, action = 2)
dataset2 # 查看dataset2数据集
BodyWgt BrainWgt NonD Dream Sleep Span Gest Pred Exp Danger
1 6654.000 5712.00 3.2 0.5 3.3 38.6 645.0 3 5 3
2 1.000 6.60 6.3 2.0 8.3 4.5 42.0 3 1 3
3 3.385 44.50 10.4 2.1 12.5 14.0 60.0 1 1 1
4 0.920 5.70 13.2 3.1 16.5 7.0 25.0 5 2 3
5 2547.000 4603.00 2.1 1.8 3.9 69.0 624.0 3 5 4
6 10.550 179.50 9.1 0.7 9.8 27.0 180.0 4 4 4
7 0.023 0.30 15.8 3.9 19.7 19.0 35.0 1 1 1
8 160.000 169.00 5.2 1.0 6.2 30.4 392.0 4 5 4
9 3.300 25.60 10.9 3.6 14.5 28.0 63.0 1 2 1
10 52.160 440.00 8.3 1.4 9.7 50.0 230.0 1 1 1
11 0.425 6.40 11.0 1.5 12.5 7.0 112.0 5 4 4
12 465.000 423.00 3.2 0.7 3.9 30.0 281.0 5 5 5
13 0.550 2.40 7.6 2.7 10.3 13.0 19.0 2 1 2
14 187.100 419.00 3.2 0.5 3.1 40.0 365.0 5 5 5
15 0.075 1.20 6.3 2.1 8.4 3.5 42.0 1 1 1
16 3.000 25.00 8.6 0.0 8.6 50.0 28.0 2 2 2
17 0.785 3.50 6.6 4.1 10.7 6.0 42.0 2 2 2
18 0.200 5.00 9.5 1.2 10.7 10.4 120.0 2 2 2
19 1.410 17.50 4.8 1.3 6.1 34.0 28.0 1 2 1
20 60.000 81.00 12.0 6.1 18.1 7.0 28.0 1 1 1
21 529.000 680.00 11.0 0.3 10.7 28.0 400.0 5 5 5
22 27.660 115.00 3.3 0.5 3.8 20.0 148.0 5 5 5
23 0.120 1.00 11.0 3.4 14.4 3.9 16.0 3 1 2
24 207.000 406.00 10.6 1.3 12.0 39.3 252.0 1 4 1
25 85.000 325.00 4.7 1.5 6.2 41.0 310.0 1 3 1
26 36.330 119.50 9.5 3.1 13.0 16.2 63.0 1 1 1
27 0.101 4.00 10.4 3.4 13.8 9.0 28.0 5 1 3
28 1.040 5.50 7.4 0.8 8.2 7.6 68.0 5 3 4
29 521.000 655.00 2.1 0.8 2.9 46.0 336.0 5 5 5
30 100.000 157.00 10.0 0.3 10.8 22.4 100.0 1 1 1
31 35.000 56.00 3.3 0.5 3.9 16.3 33.0 3 5 4
32 0.005 0.14 7.7 1.4 9.1 2.6 21.5 5 2 4
33 0.010 0.25 17.9 2.0 19.9 24.0 50.0 1 1 1
34 62.000 1320.00 6.1 1.9 8.0 100.0 267.0 1 1 1
35 0.122 3.00 8.2 2.4 10.6 7.0 30.0 2 1 1
36 1.350 8.10 8.4 2.8 11.2 4.7 45.0 3 1 3
37 0.023 0.40 11.9 1.3 13.2 3.2 19.0 4 1 3
38 0.048 0.33 10.8 2.0 12.8 2.0 30.0 4 1 3
39 1.700 6.30 13.8 5.6 19.4 5.0 12.0 2 1 1
40 3.500 10.80 14.3 3.1 17.4 6.5 120.0 2 1 1
41 250.000 490.00 8.6 1.0 9.6 23.6 440.0 5 5 5
42 0.480 15.50 15.2 1.8 17.0 12.0 140.0 2 2 2
43 10.000 115.00 10.0 0.9 10.9 20.2 170.0 4 4 4
44 1.620 11.40 11.9 1.8 13.7 13.0 17.0 2 1 2
45 192.000 180.00 6.5 1.9 8.4 27.0 115.0 4 4 4
46 2.500 12.10 7.5 0.9 8.4 18.0 31.0 5 5 5
47 4.288 39.20 11.0 1.5 12.5 13.7 63.0 2 2 2
48 0.280 1.90 10.6 2.6 13.2 4.7 21.0 3 1 3
49 4.235 50.40 7.4 2.4 9.8 9.8 52.0 1 1 1
50 6.800 179.00 8.4 1.2 9.6 29.0 164.0 2 3 2
51 0.750 12.30 5.7 0.9 6.6 7.0 225.0 2 2 2
52 3.600 21.00 4.9 0.5 5.4 6.0 225.0 3 2 3
53 14.830 98.20 2.1 0.5 2.6 17.0 150.0 5 5 5
54 55.500 175.00 3.2 0.6 3.8 20.0 151.0 5 5 5
55 1.400 12.50 10.0 0.9 11.0 12.7 90.0 2 2 2
56 0.060 1.00 8.1 2.2 10.3 3.5 60.0 3 1 2
57 0.900 2.60 11.0 2.3 13.3 4.5 60.0 2 1 2
58 2.000 12.30 4.9 0.5 5.4 7.5 200.0 3 1 3
59 0.104 2.50 13.2 2.6 15.8 2.3 46.0 3 2 2
60 4.190 58.00 9.7 0.6 10.3 24.0 210.0 4 3 4
61 3.500 3.90 12.8 6.6 19.4 3.0 14.0 2 1 1
62 4.050 17.00 11.0 2.1 12.8 13.0 38.0 3 1 1我们可以看到插补后的第2个数据集中包含62行完整的数据,如果你对第二个数据集不满意,也可以换成其它4个数据集中的任意一个。
有了无缺失值的数据集后,我们就可以放心地进行完整地分析啦!最后放上《R语言实战》中的一句话:
我相信在不久的将来,多重插补法将会得到广泛的应用。
参考文献:
Kabacoff, R. I. (2015). R in action :data analysis and graphics with r. Pearson Schweiz Ag, 1-474.