效应量：Cohen’s d与η2

参考文献：https://www.shangyexinzhi.com/article/1623003.html

导读

在文献中，我们经常会遇到Cohen’s d与η2两个指标值，其有何实际意义或作用？

解析

效应量(Effect Size, ES)，也称效果量，不依赖于样本量的影响(或者影响很小)，是衡量自变量和因变量关联强度的指标，即反映统计检验效果大小或处理效应大小，它表示不同处理下的总体平均数之间差异的大小，可以在不同研究之间进行比较。

一方面，通过效应量可以了解自变量作用的大小，还可以区分统计显著性和实际效果。统计显著性指统计结果在0.05、0.01或0.001水平上显著，但统计上显著不代表实际结果也显著，因为统计显著性容易受样本量的影响，样本量越大，结果越容易显著，而效应量基本不受样本量的影响，因此，可以更准确反映自变量对因变量的影响大小。

简言之，统计显著性表示自变量有无作用，效应量表示自变量作用的大小，所以，效应量的测量正好是对统计显著性检验的补充。在同一个实验中，如果有几个自变量，可以根据效应量将自变量的重要性排序。

另一方面，效应量的计算还可以为改进研究设计、提高检验力提供了根据。例如，独立样本t 检验发现，t 值不足以拒绝虚无假设，即差异不显著。这时可以计算效应量，如计算出的效应量的值达到中等以上，就可以通过增加实验中的样本容量的办法再进行实验，这时候就能够拒绝虚无假设，达到显著性水平。 常用的效应量指标有Cohen’s d与η2，但二者应用于不同的统计方法。

Cohen’s d反映了两个总体受某种事物的影响后的差异程度，是t检验常用效应量指标。平均数差异检验的效果大小一般用符号“d”表示 。

判定标准：

Cohen’s d值	效应量（Effect Size）
0.01-0.2	非常小
0.2-0.5	小
0.5-0.7	中等
0.8-1.2	大
1.2-2.0	非常大
2.0+	巨大

公式：

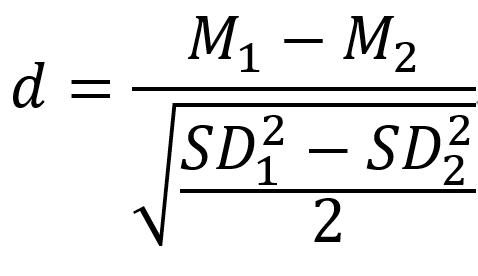
注：d = Cohen’s d 值(标准化平均偏差)，M1、M2 分别是第一个和第二个数据组的平均值，SD1、 SD2分别是第一个和第二个数据组的标准差。

η^2(eta- squared)，也是效应量的一种，它属于样本统计量，用来解释样本自变量的效果，是方差分析的常用效应量指标。η^2越大, 说明自变量的效果就越大, 自变量对因变量越重要。如果η^2很小, 即使有统计上的显著性, 也没有实际效果。

判定标准：

η^2= 0.04(效果小)；η^2= 0.25(效果中)；η^2= 0.64(效果大)。

补充内容：

如何增加效应量？在研究设计中，要想办法尽量提高统计检验能力(power of statistics test) 。但是影响统计检验能力的因素除了有统计检验方法、设定的显著性水平和样本大小以外，效应量是一个不可忽视的因素。效应量是与实验设计有关的。研究表明，在实 验中出现的误差越大，效应量越小。要增加效应量，就要进一步搞好研究设计，减少抽样误差、测量误差、操纵本身出现的误差等。