Lasso方法简要介绍及其在回归分析中的应用

回归分析（Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。最早形式的回归分析可以追溯到两百多年前由德国数学家高斯提出的最小二乘法。而回归分析也是研究时间最长和应用最广泛的的方法。自从产生以来回归分析一直都是统计学家研究的一个重点领域，直到近二十多年来还有很多对回归分析提出的各种新的改进。回归模型一般假设响应变量（response variable）也叫自变量和独立变量（independent variables）也叫因变量，有具体的参数化（parametric）形式的关系，而这些参数有很多成熟的方法可以去估计（比如最小二乘法），误差分析方法也有详细的研究。总的来说，回归分析方法具有数据适应性强，模型估计稳定，误差容易分析等优良特点，即使在机器学习方法发展如此多种多样的今天，依然是各个领域中最常用的分析方法之一。

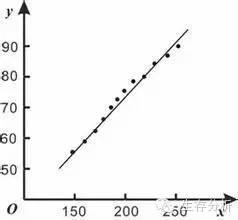
回归分析中最常见的线性回归假设响应和独立变量间存在明显的线性关系。如图1所示，响应变量（黑点）的数值大致在一条直线周围，除了每个点都有的随机误差。线性回归模型看似极大的简化了响应变量和独立变量之间的关系，其实在实际分析中往往是最稳定的模型。因为线性模型受到极端或者坏数据的影响最小。例如预测病人的住院成本，很可能出现其中一两个病人会有很大的花费，这个可能是跟病理无关的，这种病人的数据就很可能影响整个模型对于一般病人住院成本的预测。所以一个统计模型的稳定性是实际应用中的关键：对于相似的数据应该得出相似的分析结果。这种稳定性一般统计里用模型的方差来表示，稳定性越好，模型的方差越小。

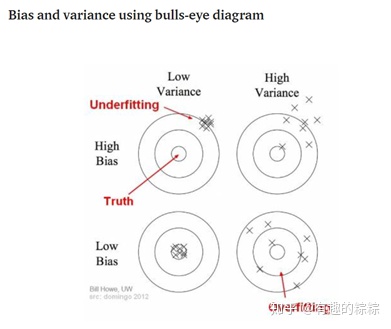
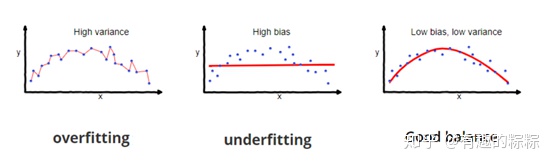
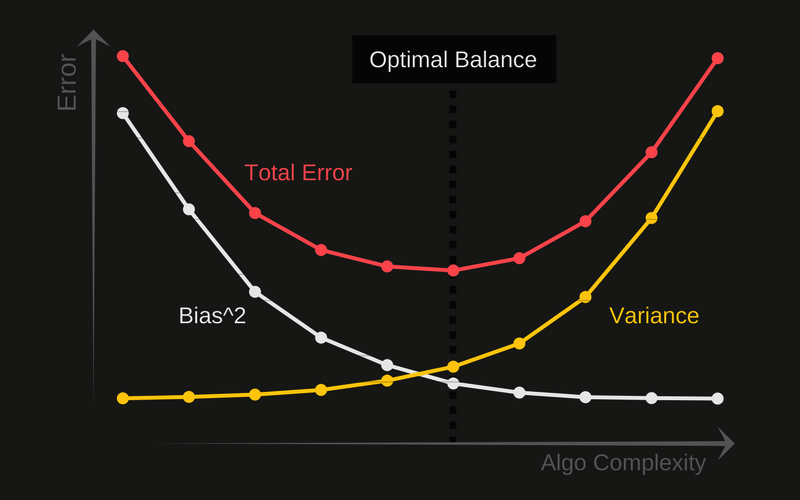
在统计学习中存在一个重要理论：方差权衡。一般常理认为模型建立得越复杂，分析和预测效果应该越好。而方差权衡恰恰指出了其中的弊端。复杂的模型一般对已知数据（training sample）的拟合（fitting）大过于简单模型，但是复杂模型很容易对数据出现过度拟合（over-fitting）。因为所有实际数据都会有各种形式的误差，过度拟合相当于把误差也当做有用的信息进行学习。所以在未知数据（test sample）上的分析和预测效果会大大下降。图二说明了方差权衡的结果。模型复杂度在最低的时候（比如线性回归）预测的偏差比较大，但是方差很小。随着模型复杂度的增大，对已知数据的预测误差会一直下降（因为拟合度增大），而对未知数据却出现拐点，一旦过于复杂，预测方差会变大，模型变得非常不稳定。

因此在很多实际生活应用中，线性模型因为其预测方差小，参数估计稳定可靠，仍然起着相当大的作用。正如上面的方差权衡所述，建立线性模型中一个重要的问题就是变量选择（或者叫模型选择），指的是选择建立线性模型所用到的独立变量的选择。在实际问题例如疾病风险控制中，独立变量一般会有200 ~ 300个之多。如果使用所有的变量，很可能会出现模型的过度拟合。所以对变量的选择显得尤为重要。

传统的变量选择是采用逐步回归法（stepwise selection），其中又分为向前（forward）和向后（backward）的逐步回归。向前逐步是从0个变量开始逐步加入变量，而向后逐步是从所有变量的集合开始逐次去掉变量。加入或去掉变量一般按照标准的统计信息量来决定。这种传统的变量选择的弊端是模型的方差一般会比较高，而且灵活性较差。近年来回归分析中的一个重大突破是引入了正则化回归（regularized regression）的概念, 而最受关注和广泛应用的正则化回归是1996年由现任斯坦福教授的Robert Tibshirani提出的LASSO回归。LASSO（Least Absolute Shrinkage and Selection Operator）回归最突出的优势在于通过对所有变量系数进行回归惩罚（penalized regression）, 使得相对不重要的独立变量系数变为0，从而排除在建模之外。

LASSO方法不同于传统的逐步回归的最大之处是它可以对所有独立变量同时进行处理（图三），而不是逐步处理。这一改进使得建模的稳定性大大增加。除此以外，LASSO还具有计算速度快，模型容易解释等很多优点。而模型发明者Tibshirani教授也因此获得当年的有统计学诺贝尔奖之称的考普斯总统奖（COPSS award）。

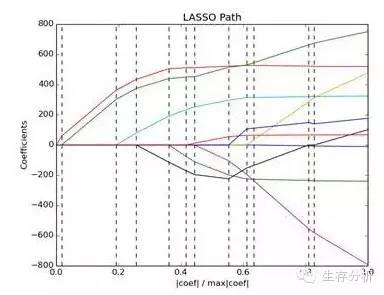
对于图3简要说明一下，横轴代表模型系数比，纵轴代表系数，图中的每一条彩色实线代表一个变量，竖向的虚线代表一个惩罚值（后面会介绍），其筛选变量的过程，就是有一个指标（CV）最小时，其对应会有个惩罚值，用此惩罚值去画一条虚线，与彩色线相交的即为筛选到的变量。诸如第二条虚线与两条彩色线相交，即筛选到两个变量。

说到这里不得不说说，与Lasso类似的岭回归，对于岭回归想必大家有所耳闻，其在线性回归学习中，对出现多重共线性问题时，老师给出的意见是用岭回归。当多重共线性问题存在时，就连最基本的最小二乘估计都是有偏的，线性模型估计系数的方差将会很大，这表示分析结果可能远远偏离真实的水平。岭回归通过添加一种调整参数（也叫惩罚）对有偏的部分进行压缩，使其尽可能的小，从而起到校正模型的作用。为了解决多重共线性问题，岭回归通过将调整参数λ引入模型。

类似于岭回归，Lasso方法也对回归系数的绝对规模采取了惩罚的形式。同时，它还能减少变异性并提高模型的精度。

由上式可见，Lasso回归与岭回归的不同之处在于其在惩罚函数中使用了绝对值而非平方和的形式，这将导致在模型的参数估计过程中有些系数会因为惩罚项的存在从而直接减少到0。随着惩罚力度的增强，越来越多的系数将会缩小并最终归结为0，这意味着在模型构建的同时我们也对原本给定的多个变量进行了变量选择。

这一方法在临床医学的应用，最早是由Tibshirani教授本人将其用于COX回归中。在其文献中，作者首先用Lasso筛选出有意义的变量，注意这里选出的变量会与COX本身用的Stepwise方法筛选的不一样，进一步将筛选出的变量建立COX模型，看新的模型与原先Stepwise方法筛选建立的模型比对，发现新的模型更有意义，筛选的变量更贴近实际。

在临床应用中，如果研究者在筛选变量时得不到自己想要的结果，或者说自变量间存在多重共线性时，这一方法会是个不错的选择。另有研究显示这一方法用于高维度（变量个数远大于样本量）强相关、小样本的生存资料分析非常有效。这种数据资料往往在基因数据中比较常见。